Модифицированный имитационным моделированием метод экспоненциального сглаживания

, (4.35)

где – степенной определитель -го порядка (4.29), значение которого вычисляется методом перекрестного умножения (блоки 19, 20);

– определитель, получаемый из (4.29) заменой -й строки на функции – блок 23;

– вычисленная ранее производная.

Значение функции в каждой точке и ее отклонения вычисляются в блоках 21, 22, 24-26. При подстановке значений , и зависимость (4.35) принимает вид суперпозиции экспоненциальных законов, параметрами которых являются аргументы прогнозирующих зависимостей.

Если все корни комплексные, то имеет вид

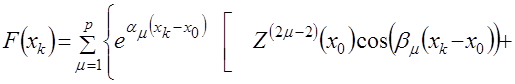
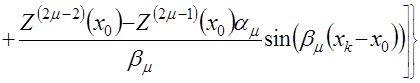,(4.36)

где – нечетное натуральное число;

– действительная часть корня; ; .

Значения функции и ее отклонения вычисляются в блоках 28, 29. Если в результате анализа устанавливается, что корней комплексные, а корней действительные, то принимает вид

,

где вычисляется по зависимости (4.36) с использованием корней блок 38); при вычисляется по зависимости (4.35) с использованием корней (блоки 33, 34, 35, 41), при – в соответствии с блоками 32, 39, 40. Значения функции и ее отклонения от вычисляются в блоках 36, 37, 42, 43, 44. Результаты расчетов выводятся на печать. После вычисления функции и в каждом из приведенных случаев выбирается максимальное значение отклонения , которое сравнивается с заданным (блоки 45, 47).

Актуально о образовании:

Методики диагностики уровня развития самостоятельности у детей младшего дошкольного возраста
На основе изученной литературы, мною была составлена следующая анкета для воспитателей младшей группы детского сада по поводу сформированности умений у детей младшего дошкольного возраста в художественном творчестве. Анкета для воспитателей. На основе наблюдения оцените следующие умения по пятибалл ...

Методы воспитательной работы с младшими школьниками в условиях дополнительного образования
педагогический школьник внеклассный образование Содержание и многообразие форм учебно-воспитательного процесса в их единстве позволяет заинтересовать и вовлечь детей в систему дополнительного образования. Разнообразие форм даёт возможность увеличить число воспитывающих факторов, влияющих на сознани ...

Психолого-педагогические основы воспитания этической культуры младших школьников
Наиболее высоким уровнем нравственной воспитанности личности является её способность ориентироваться соответствующим нормам морали. Нравственно воспитанным является такой человек, который не только усвоил нравственные знания, но и ведет себя в любых ситуациях в соответствии с ними. У нравственно во ...