Модифицированный имитационным моделированием метод экспоненциального сглаживания

Известно что любой процесс можно представить в

, (4.17)

где – исходный процесс (функция одного переменного);

– приближенная модель процесса (описание с помощью ФГС);

– остаток (некоторая функция точности приближения).

В наиболее общем виде ФГС для одного аргумента записывается в виде [1], [2]

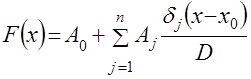, (4.18)

где – некоторое фиксированное натуральное число;

– начальное значение фактора-аргумента на рассматриваемом интервале;

– постоянные действительные параметры;

– специальный (степенной) определитель -го порядка;

– функция, получаемая из определителя заменой строки на соответствующие функции

, .

При функция с гибкой структурой имеет вид

, (4.19)

где – начальное значение функции и ее производной в точке ; – корень специального уравнения , в рассматриваемом случае .

Нахождение параметров функции связано с минимизацией базисной функции

. (4.20)

Далее представляется логичным определить порядок расчета параметров ФГС. В том случае, когда имеется всего один фактор, базисная функция имеет вид

. (4.21)

При на рассматриваемом отрезке функция равна нулю, и если проинтегрировать выражение (2.4.21) для того, чтобы избавиться от производных, можно получить

. (4.22)

Подставляя в это уравнение значение начальной точки, легко установить, что величина первой производной связана со значением величины и соотношением . (4.23)

Если проинтегрировать уравнение (22) еще раз, то можно записать выражение вида

. (4.24)

При условии, что , определяется . Тогда уравнение (4.24) целесообразно представить следующей зависимостью:

Актуально о образовании:

Анализ результатов диагностики особенностей лексической стороны речи детей контрольной группы
В экспериментальном исследовании с целью изучения особенностей лексической стороны речи у детей 5 - 6 лет мы применили диагностические методики Е.Ф. Архиповой[2] «Исследование семантической структуры слова и лексической системности»: · методика №1 «Классификация понятий», · методика № 2 «Подбор ант ...

Анализ психолого-педагогической литературы по проблеме обучения детей иностранному языку
Экономический рост и развитие торговых отношений между различными странами выдвигает на первое место вопрос о межнациональном общении. Уже в прошлом столетии многие педагоги задумывались над проблемой обучения детей иностранному языку. Тихеева Е.И. в своей книге «Развитие речи детей» говорит о том, ...

Учебный план
Учебный план представляет собой основной (исходный) документ, на основе которого осуществляется вся многогранная работа по физическому воспитанию, определяется основное направление и продолжительность учебной работы для того или иного контингента занимающихся. Он предусматривает последовательность ...