Что понимается под названием вычислительный эксперимент

Вероятность называют доверительной вероятностью, а границы интервала , в которых с заданной доверительной вероятностью заключена ошибка метода – доверительными границами.

Из теории вероятностей известно, что при нормальном законе распределения вероятность отклонения случайной величины от ее математического ожидания менее, чем на равна

, (4)

где – функция Лапласа (интеграл вероятностей);

– аргумент функции Лапласа;

– среднее квадратическое отклонение величины .

Также известно, что если производится большое число опытов, то среднее арифметическое есть также случайная величина, приближенно распределенная по нормальному закону с математическим ожиданием и средним квадратическим отклонением .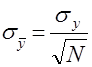

Из сказанного следует, что вероятность любого отклонения может быть вычислена по формуле

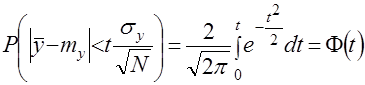. (5)

Положим

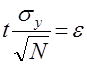, (6)

тогда получим

. (7)

Сравнивая выражения (3) и (7), найдем условие, при котором ошибка метода не превысит величину с вероятностью :

. (8)

Задаваясь доверительной вероятностью , найдем из уравнения (8) с помощью таблиц функции Лапласа численное значение . Подставив далее величину в выражение (6), получим формулу для вычисления искомого числа испытаний , при котором выполняется условие (8):

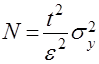. (9)

Из формулы (9) видно, что для определения необходимо еще знать величину дисперсии . Так как она неизвестна, обычно поступают следующим образом. Задаются некоторым достаточно большим значением и находят приближенное значение (статистическую оценку) дисперсии по формуле

Актуально о образовании:

Д.И. Менделеев о народном образовании
Он постоянно проводил мысль, что школа – это громадная сила, определяющая судьбы народов и государств, считал, что без расширения народного просвещения невозможно и само развитие России. В статьях и речах о состоянии и развитии образования в России Д. И. Менделеев высказывал следующие принципиальны ...

Оценка педагогических идей М. Монтессори её современниками
Мария Монтессори была первой женщиной-врачом в Италии. Начав работать ассистентом врача в университетской клинике, она заинтересовалась методами лечения и реабилитации детей с ограниченными умственными способностями. Монтессори пришла к выводу, что проблемы умственно отсталых детей - это проблемы н ...

Межпредметные связи в курсе школьного предмета химии
Межпредметные связи – это современный принцип обучения в средней школе. Он обеспечивает взаимосвязь предметов естественнонаучного и естественно-гуманитарного циклов и их связь с трудовым обучением школьников. По определению Д. П. Ерыгина: «Межпредметные связи можно рассматривать как дидактическую с ...