Что понимается под названием вычислительный эксперимент

Статистическая обработка и оценка точности результатов моделирования основывается на предельных теоремах теории вероятностей: теореме Чебышева и теореме Бернулли.

Согласно теореме Чебышева, при неограниченном увеличении числа независимых испытаний среднее арифметическое значение случайной величины сходится по вероятности к математическому ожиданию этой величины, то есть

, (1)

где – сколь угодно малое положительное число,

.

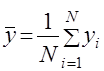Теорема Бернулли доказывает, что при неограниченном увеличении числа независимых испытаний частота наступления случайного события сходится к вероятности этого события, то есть

. (2)

Пусть случайная величина характеризуется математическим ожиданием и дисперсией . В качестве приближенного значения величины берется среднее арифметическое значение , определяемое по результатам независимых испытаний. Отклонение величины от искомого математического ожидания и есть ошибка метода. Величина , удовлетворяющая неравенству , называется точностью оценки.

Из теоремы Чебышева следует, что ошибка метода может быть оценена лишь вероятностно, с определенной степенью достоверности. Обозначим через вероятность того, что выполняется неравенство :

. (3)

Вероятность характеризует степень достоверности оценки, ее надежность. Это означает, что с надежностью можно быть уверенным, что среднее арифметическое значение не выйдет за пределы интервала , то есть, что

.

Актуально о образовании:

Задачи, решаемые с помощью таблиц
При подготовке к решению таких задач можно удачно использовать карты сигналы (см. рис. 1). №1 на…больше + №2 в…больше Х №3 на…меньше – №4 в…меньше : Рис. 1. Карты сигналы Устный счет следует проводить с использованием данных карт, которые должны быть у каждого учащегося, что позволяет привлечь к ра ...

Связь и различие эстетического и художественного воспитания и образования
Для отечественной педагогической мысли характерна постановка проблемы формирования и развития эстетического потенциала личности. Уже в 1890 году русский педагог В.П.Острогорский в "Письмах об эстетическом воспитании" обращал, внимание на то, что в школе необходимо не только формально разв ...

Классификация ошибок наиболее часто встречающихся у учащихся 5-6 классов
Во время пассивной практики, на 3 и 4 курсе, а также при посещении уроков, которые давали студенты педагогического университета, мы провели предварительные исследования, постаравшись выявить наиболее характерные ошибки, которые делают при продуцировании в устном и письменном высказывании учащиеся 5 ...